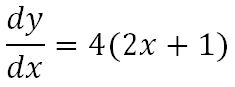Primero debemos aclarar lo que es una función compuesta. Una función compuesta es una función dentro de otra función, por ejemplo
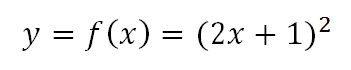
Aquí vemos que la “función interna” es una función lineal
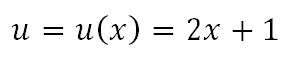
Mientras que la “función interna” está dentro de la función f(x)=f(u) que es una función cuadrática y la llamaremos “función externa”
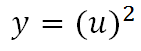
La regla de la cadena nos dice que la siguiente fórmula
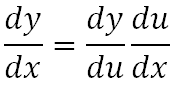
Y la usaremos para derivar la función y=f(x)
Otra de forma de escribir la regla de la cadena es la siguiente
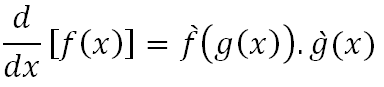
En esta forma podemos decir que para derivar una función compuesta multiplicamos la derivada de la función externa por la derivada de la función interna
Nota: Debemos tener en cuenta las diferentes formas de denotar la derivada de una función f(x), estas son
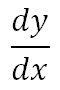
Y
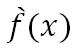
Ejemplo:
Derivar la función
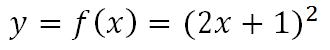
Usando la regla de la cadena
Solución:
Sabemos que la “función interna” es
![]()
Además la “función externa” es
![]()
Calculamos la derivada de esta función usando la Tabla de Derivadas
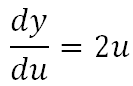
Calculamos la derivada de la función interna u(x) usando la Tabla de Derivadas
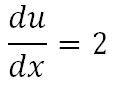
Usamos la regla de la cadena
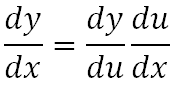
Reemplazando las derivadas calculamos que
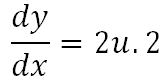
Remplazamos el valor de u y organizamos los términos