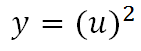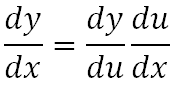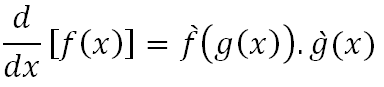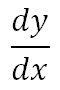Cálculo Diferencial

Cálculo del límite de una función por factorización

Para calcular el límite de una función en la que obtenemos una indeterminación del tipo 0/0, en la mayoría de los casos cuando se trata de funciones racionales, podremos eliminar la indeterminación factorizando tanto el numerador como el denominador, si el problema lo permite y eliminando los factores que tienen dicha indeterminación.

Este proceso quedará más claro si vez el siguiente video, donde resolvemos un ejercicio de este tipo. No te pierdas el vídeo y te invito a aprender cálculo.

Encuentre la ecuación de la recta tangente y de la recta normal a la curva dada

Para encontrar la ecuación de la recta tangente y de la recta normal a la curva dada, en un
punto de abscisa dado, seguimos los siguientes pasos.

Paso 1: Primero encontramos la derivada de la ecuación que nos proporcionan. Esta ecuación puede ser del tipo “y” es igual a, o también una relación de “y” y “x” donde no se encuentra despejada y, en estos casos debemos usar derivación implícita.

Paso 2: Despejamos la derivada.

Paso 3: Evaluamos la derivada en el punto dado, el valor que obtenemos corresponde a la pendiente de la recta tangente a la curva en el punto dado.

Paso 4: Usamos la fórmula de la ecuación de la recta Punto-Pendiente para encontrar la ecuación de la recta tangente.

Paso 5: Teniendo en cuenta que el producto de las pendientes de la recta tangente y la recta normal da -1 calculamos la pendiente de la recta normal.

Paso 6: Usamos de nuevo la ecuación de la recta Punto-Pendiente para encontrar la ecuación de la recta normal.

Mira el siguiente vídeo en el que hemos resuelto un ejercicio siguiendo todos los pasos descritos anteriormente.

Demostración de la derivada de funciones trigonométricas inversas

Si alguna vez haz intentado realizar una demostración matemática, seguro te habrás dado cuenta que a veces resulta difícil saber que camino tomar.

En este post vamos a aprender que debemos hacer para deducir las fórmulas de las derivadas de las funciones trigonométricas inversas. Primero vamos a describir dichas formulas y posteriormente su deducción en un conjunto de 6 vídeos.

Espesemos con la fórmula de la derivada de la función seno inverso:

En este caso debemos interpretar D_x como la derivada con respecto a x

Mira ahora el vídeo para la demostración de la derivada de la función seno inverso

Veamos ahora ahora la fórmula de la derivada de la función coseno inverso:

Mira ahora el vídeo para la demostración de la derivada de la función coseno inverso

Fórmula de la derivada de la función tangente inverso:

Mira ahora el vídeo para la demostración de la función tangente inverso

Fórmula de la derivada de la función cosecante inverso:

Mira ahora el vídeo para la demostración de la función cosecante inverso

Fórmula de la derivada de la función secante inverso:

Mira ahora el vídeo para la demostración de la función secante inverso

Fórmula de la derivada de la función cotangente inverso:

Mira ahora el vídeo para la demostración de la función cotangente inverso

Regla de la cadena o derivada de una función compuesta

Primero debemos aclarar lo que es una función compuesta. Una función compuesta es una función dentro de otra función, por ejemplo

Aquí vemos que la “función interna” es una función lineal

Mientras que la “función interna” está dentro de la función f(x)=f(u) que es una función cuadrática y la llamaremos “función externa”

La regla de la cadena nos dice que la siguiente fórmula

Y la usaremos para derivar la función y=f(x)

Otra de forma de escribir la regla de la cadena es la siguiente

En esta forma podemos decir que para derivar una función compuesta multiplicamos la derivada de la función externa por la derivada de la función interna

Nota: Debemos tener en cuenta las diferentes formas de denotar la derivada de una función f(x), estas son